计算机图形学，computer-graphics，简称cg

看了GAMES101-现代计算机图形学入门，做下笔记

2D和3D点的表示 #

计算机图形学中有个有趣的表示，那就是用向量和他的冗余值来表示对象，举例子来说,[2,1,1]表示点(2,1)，[2,1,0]表示向量(2,1)，两者的不同在于后者的冗余表示为0.

冗余值对于线性代数中的计算非常有帮助。

比如下面就是一个先逆时针旋转45度，再移动(1,0)的例子。

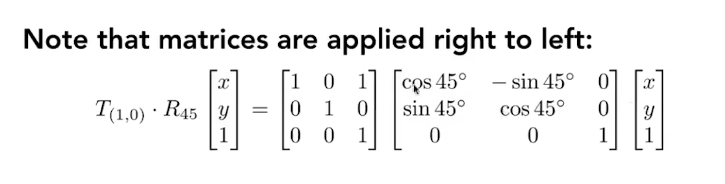
由于冗余1的存在，在线代计算中，变换矩阵的最后一列就有了意义。

2D点旋转与移动 #

用了Eigen作为线性代数运算库，官方文档为http://eigen.tuxfamily.org。

下面我们要把一个点(2,1)，先逆时针旋转45度，再平移(1,2)，那么数学上的运算就是3个矩阵相乘。三维上会复杂点，但基本原理差不多。

constexpr double PI = 3.1415926535;

double angle = 45;
double radian = angle * PI / 180.0f;
Eigen::Vector3f p(2.0f, 1.0f, 1.0f);    // 点(2,1)

// 旋转
Eigen::Matrix3f r3;
r3 << std::cos(radian), -std::sin(radian), 0,
    std::sin(radian), std::cos(radian), 0,
    0, 0, 1;

// 位移
Eigen::Matrix3f m3;
m3 << 1, 0, 1,
    0, 1, 2,
    0, 0, 1;

p = r3 * p;     // 先逆时针旋转45度

p = m3 * p;     // 再位移(1,2)

3D旋转 #

下面绕z轴逆时针旋转45度的计算矩阵，这里注意，绕那个轴，哪个轴对应的计算矩阵的行列值为单位矩阵值。

[cos(45),-sin(45),0,0,
 sin(45),cos(45),0,0
    0,    0,    1,    0,
    0,    0,    0,    1]

未完待续:2021-05-02

REF #

• 计算机图形学与混合现实研讨会