并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
算法思想 #
用集合中的某个元素来代表这个集合,,该元素称之为集合的代表元
每个集合可以理解为一个树,对于集合中的每个元素(如x),都有一个值(如parent[x])指向其在结构上的父节点。如果x为集合的代表元,即根节点,则令parent[x]=x;
对于查找操作,假设需要确定x所在的的集合,也就是确定集合的代表元。可以沿着parent[x]不断在树形结构中向上移动,直到到达根节点。
判断两个元素是否属于同一集合,只需要看他们的代表元是否相同即可。
并查集的三个操作 #
- 初始化
- 查找
- 合并集合
初始化 #
包括对所有单个的数据建立一个单独的集合(即根据题目的意思自己建立的最多可能有的集合,为下面的合并查找操作提供操作对象)
结构体表示法 #
#define MAX 10000
struct Node
{
int parent; // 集合index的类别
int data; // 集合index的数据类型
int rank; // 集合index的层次,通常初始化为0
}node[MAX];
// 初始化i集合的函数
void init(int i){
node[i].parent=i; // 初始化的时候,一个集合的parent都是这个集合自己的标号。
// 没有跟它同类的集合,那么这个集合的源头只能是自己了。
node[i].rank=0;
}
数组表示法 #
int parent[max];
int rank[max];
int data[max];
void init(int i)
{
set[i]=i;
rank[i]=0;
}
查找 #
结构体 #
/**
*查找集合i(一个元素是一个集合)的源头(递归实现)。
如果集合i的父亲是自己,说明自己就是源头,返回自己的标号;
否则查找集合i的父亲的源头。
**/
int get_Parent(int x)
{
if(node[x].parent==x)
{
return x;
}
// 在进行查找时,顺便压缩路径
node[x].parent = get_Parent(node[x].parent);
return node[x].parent;
}
数组 #
// 查找集合i(一个元素是一个集合)的源头(递归实现)
int find_set(int i)
{
// 如果集合i的父亲是自己,说明自己就是源头,返回自己的标号
if(set[i]==i)
{
return set[i];
}
// 否则查找集合i的父亲的源头
return find_set(set[i]);
}
// 查找的同时进行集合的优化的函数(减少树的高度)
int unifind(int a){
int root = a;
// 找到根节点
while(root != parent[root] ){
root = parent[root];
}
// compress the path
while( a != root){
int parentOfA = parent[a];
parent[a] = root; // 将当前节点的父节点直接设置为父节点
a = parentOfA;
}
return root;
}
合并集合 #
Talk is cheep,show the code.
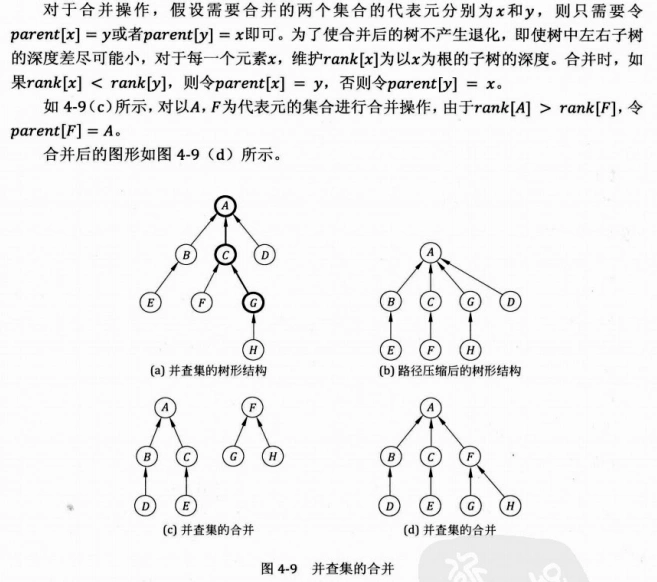
这里在合并时按照秩进行了路径压缩,将秩较小的树合并到大的上。
结构体 #
void Union(int a,int b)
{
a=get_parent(a);
b=get_parent(b);
if(node[a].rank>node[b].rank)
node[b].parent=a;
else
{
node[a].parent=b;
if(node[a].rank==node[b].rank)
{
node[b].rank++;
}
}
}
数组 #
void Union(int i,int j)
{
i=Find_Set(i);
j=Find_Set(j);
if(i==j) return ;
if(rank[i]>rank[j])
{
set[j]=i;
}
else
{
if(rank[i]==rank[j])
{
rank[j]++;
}
set[i]=j;
}
}
集合数统计 #
计算最后有多少元素父元素仍然为自己parent[x]==x,就算出有多少个不相交的集合
// 这里只放结构体的函数了
int count(int i){ // i为有效元素数目
int c=0;
while(i--){
if(node[i].parent==i){
c++;
}
}
return c;
}
ACM典型例题: acm_hdu_1213